Soft Separation and Distillation: Toward Global Uniformity in Federated Unsupervised Learning

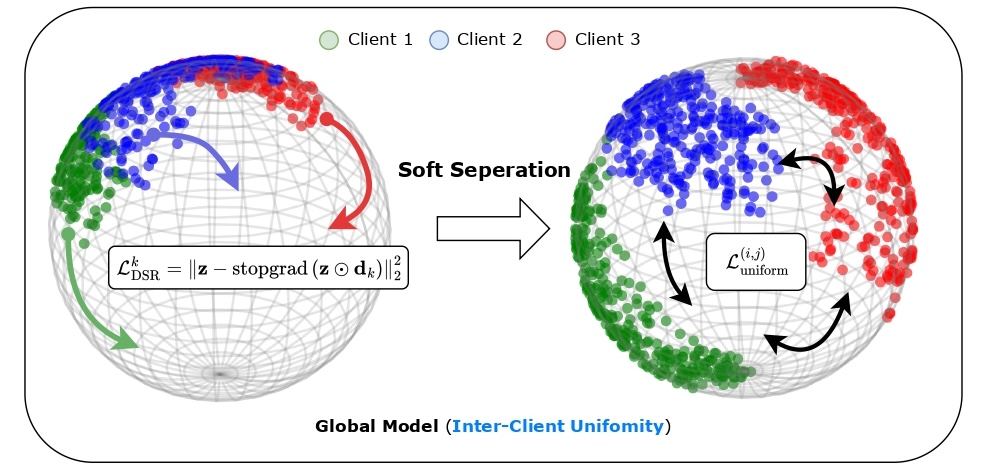
Dimensional collapse in extreme UniDA scenarios

By softly separating client representations, SSD encourages them to spread toward different directions, thereby improving global uniformity while preserving local representation expressiveness.

Motivation

Uniformity in Representation Learning

Uniformity is a critical metric in representation learning (Wang et al., 2020, Fang et al., 2024), where higher uniformity indicates better preservation of information in the learned representations. In centralized training, jointly optimizing alignment loss, which encourages closeness of similar samples, and uniformity loss, which maximizes preserved information, yields high-quality representations.

$$ \mathcal{L}_{\text{align}} = \mathbb{E}_{\mathbf{x}\sim p(\mathbf{x}), \tilde{\mathbf{x}},\tilde{\mathbf{x}}^+ \sim \mathcal{T}(\mathbf{x})} ||\mathbf{z} - \mathbf{z}^+||^2_2, \quad \mathcal{L}_{\text{uniform}} = - \log \mathbb{E}_{\mathbf{z}_i, \mathbf{z}_j \overset{\text{i.i.d}}{\sim} p(\mathbf{z})}\bigl[e^{-t ||\mathbf{z}_i - \mathbf{z}_j||^2_2}\bigr] $$

Challenges in Achieving Global Uniformity under Non-IID Data

In decentralized training with non-IID data, however, achieving global uniformity is challenging.

$$ \mathcal{L}_{\text{uniform}} = - \log \biggl( \underbrace{\sum_{k=1}^K \mathbb{E}_{\mathbf{z}, \mathbf{z}' \overset{\text{i.i.d}}\sim p_k(\mathbf{z})} [e^{-t {||\mathbf{z} - \mathbf{z}'||^2_2}}] }_{\text{intra-client } \mathcal{L}_{\text{uniform}}^k} \\ + \underbrace{\sum_{i\neq j} \mathbb{E}_{\mathbf{z} \sim p_i(\mathbf{z}), \mathbf{z}'\sim p_j(\mathbf{z})}[e^{-t {||\mathbf{z} - \mathbf{z}'||^2_2}}]}_{\text{inter-client }\mathcal{L}_{\text{uniform}}^{(i, j)}} \biggr) $$

In this setting, each client $i$ optimizes its local loss function using samples from its own data distribution $p_i$. In homogeneous settings, where client distributions are similar (i.e., $p_i \approx p_j$), optimizing intra-client uniformity naturally promotes good inter-client uniformity. However, in non-IID settings, where client distributions differ significantly, optimizing only intra-client uniformity fails to ensure good inter-client uniformity, leading to suboptimal global representation quality.

Method

The core challenge in enhancing inter-client uniformity lies in the federated learning constraint that the server has no access to raw client data or embeddings, making it impossible to directly impose a loss function that operates across different clients.

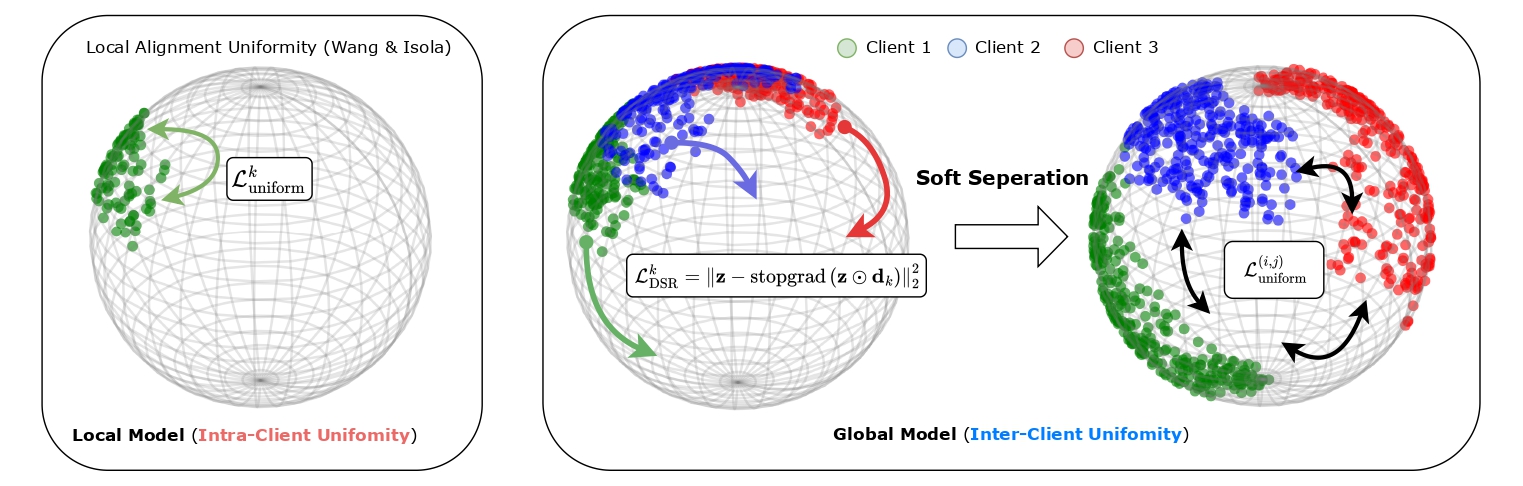
Dimensional-Scaled Regularization

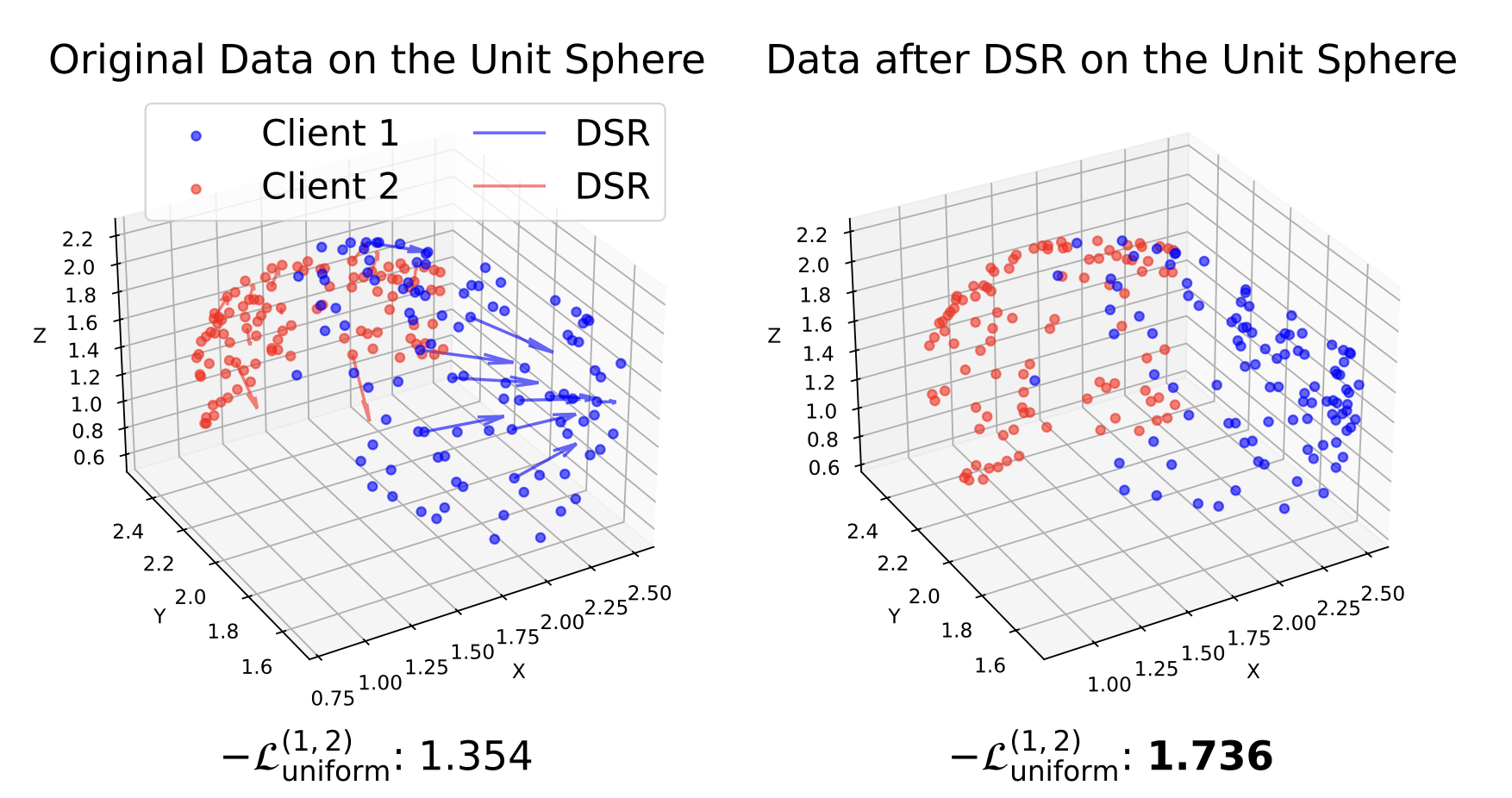
Our idea is to assign a specific direction to each client, encouraging their representations to spread toward different directions. Specifically, for each client $k$, we define a dimension-scaling vector $\mathbf{d}_k \in \mathbb{R}^d$, where $d$ is the dimensionality of the embedding space. This vector applies selective scaling to specific dimensions. We then regularize each client's embeddings by encouraging them to move toward their dimension-scaled versions through the following loss: $$ \mathcal{L}_{\text{DSR}}^k = \mathbb{E}_{\mathbf{z}\sim p_k(\mathbf{z})}\left[\|\mathbf{z} - \text{stopgrad}(\mathbf{z} \odot \mathbf{d}_k)\|_2^2\right], $$ where $\odot$ represents element-wise multiplication, and $\text{stopgrad}(\cdot)$ prevents gradient flow through the scaled target. The effect of DSR is shown below.

Projector Distillation

While DSR effectively enhances uniformity at the embedding level, we observe that this improvement may not fully transfer to the representation level. This discrepancy occurs because the projector $g(\cdot)$ placed between the encoder $f(\cdot)$ and the loss function can absorb much of the optimization effect, as shown below.

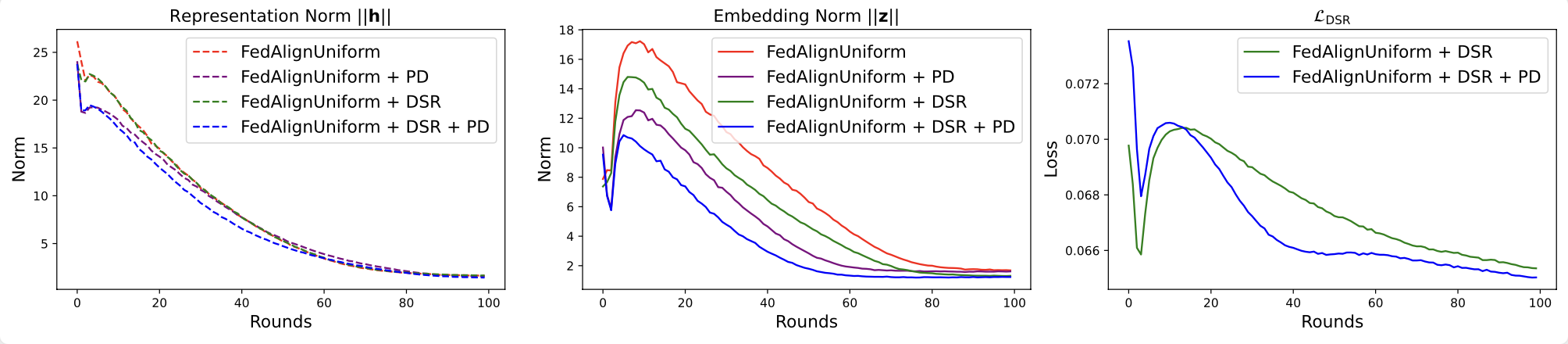
Although removing the projector might seem like a direct solution, prior work (Gupta et al., 2022, Xue et al., 2024) has shown that the projector plays a crucial role in separating optimization objectives from representation quality, thereby preventing overfitting to specific self-supervised tasks. To bridge this gap, we introduce Projector Distillation (PD), which explicitly aligns the encoder's representations $\mathbf{h}$ with the projector's embeddings $\mathbf{z}$: $$ \mathcal{L}_{\text{distill}}^k = \mathbb{E}_{x\sim p_k(\mathbf{x})}\left[D_{\text{KL}}\left(\sigma(\mathbf{h}) \| \sigma(\mathbf{z})\right)\right], $$ This distillation mechanism encourages the encoder to internalize the beneficial structure learned in the embedding space, effectively transferring the improved uniformity from embeddings to representations.

Results

Main Results

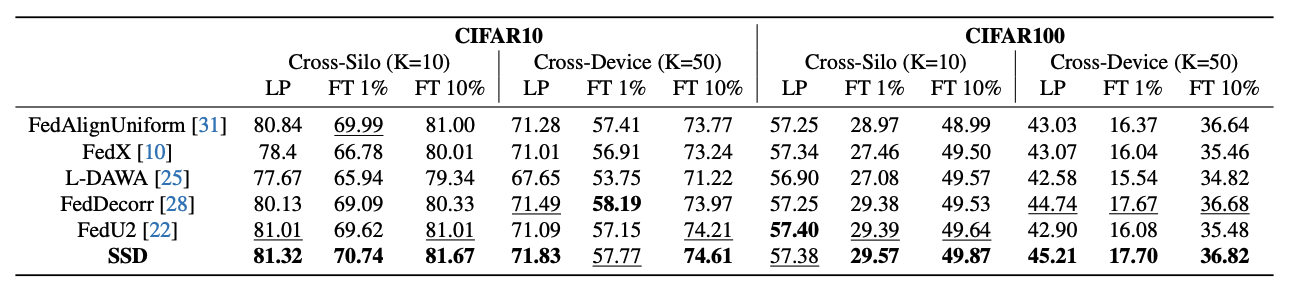
Transfer Learning

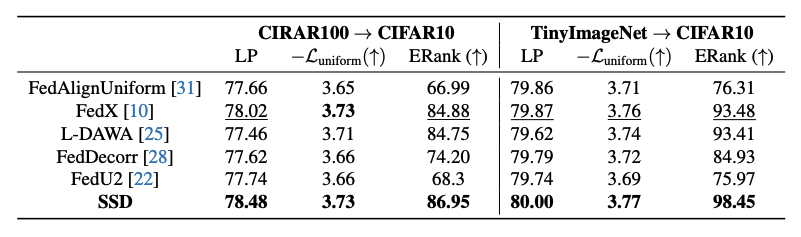
SSD shows strong transferability to out-of-distribution data, achieving better performance and representation quality. An interesting observation is that FedX, which does not perform well in the main table, shows good representation quality and strong performance in this setting. This implies a correlation between representation quality and transferability.

Soft vs. Hard Separation

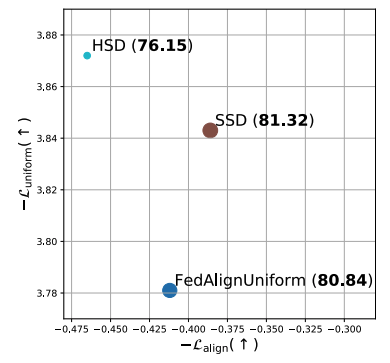
We adopt a soft separation strategy that regularizes client representations toward a specific direction. In contrast, a more direct approach to maximizing inter-client uniformity is to constrain each client to a distinct, client-specific subspace. As shown in the table, this method indeed achieves the highest uniformity, but at the cost of reduced alignment.

Why not remove the projector?

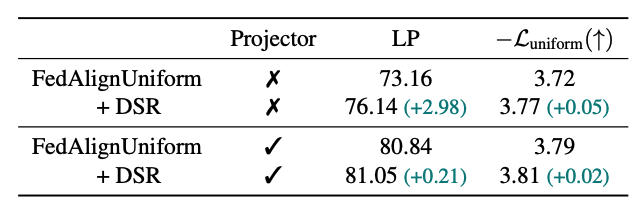
As shown in the table, removing the projector significantly improves uniformity when DSR is applied, highlighting the impact of the separation strategy. However, this also results in a substantial drop in performance. To address this, we propose a strategy that preserves the projector while still maintaining the separation effect.

BibTeX

@inproceedings{ssd_fang2025,
    title={Soft Separation and Distillation: Toward Global Uniformity in Federated Unsupervised Learning},
    author={Hung-Chieh Fang and Hsuan-Tien Lin and Irwin King and Yifei Zhang},
    booktitle={Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV)},
    year={2025},
}